Klaus Hildebrandt

Associate Professor

Computer Graphics and Visualization Group

Delft University of Technology
EEMCS - Dept. Intelligent Systems
Van Mourik Broekmanweg 6, 2628 XE Delft
Room W 5.620
Email: k.a.hildebrandt -at- tudelft -dot- nl

Klaus Hildebrandt

Short Resume

I am an Associate Professor in the Department of Intelligent Systems at Delft University of Technology. Prior to this, I was a Senior Researcher at the Max Planck Institute for Informatics in Saarbrücken, where I led the Applied Geometry group. I received my PhD from the Free University Berlin.

My research interests include Visual Computing, Geometric Data Processing, Physical Simulation, and Computational and Discrete Differential Geometry. My work has been recognized with several best paper awards at international conferences including Eurographics, ACM UIST, Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, and Solid Modeling International. I co-chaired the Eurographics Symposium on Geometry Processing in 2017, the Eurographics State-of-the-Art Reports in 2018, the Eurographics Tutorials in 2025, and the International Conference on Geometric Modeling and Processing in 2025 and 2026.

Teaching

Courses I teach regularly at TU Delft:

I serve as Director of Studies of the master's program Computer Science at TU Delft.

Publications

Geometric Multigrid Neural Networks
Jackson Campolattaro, Ruben Wiersma, Klaus Hildebrandt
Computer Aided Geometric Design, 2026
[doi]
LoGCC: Local-to-Global Correlation Clustering for Scalar Field Ensembles
Nicolas F. Chaves-de-Plaza, Renata G. Raidou, Prerak Mody, Marius Staring, René van Egmond, Anna Vilanova, Klaus Hildebrandt
IEEE Transactions on Visualization and Computer Graphics, 2026
[doi]
Application of augmented reality in robot-assisted mitral valve repair surgery: A feasibility study.
Jette J. Peek, Klaus Hildebrandt, Xucong Zhang, Rohit K. Kharbanda, Maurice A.P. Oudeman, Robert J.M. Klautz, Meindert Palmen, Edris A.F. Mahtab
Innovations: Technology and Techniques in Cardiothoracic and Vascular Surgery, 2025
[doi]
A novel 3D image registration technique for augmented reality vision in minimally invasive thoracoscopic pulmonary segmentectomy
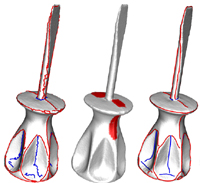
J. J. Peek, X. Zhang, K. Hildebrandt, S. A. Max, A. H. Sadeghi, A. J. J. C. Bogers, E. A. F. Mahtab
International Journal of Computer Assisted Radiology and Surgery (Springer), 2025
[video][doi]
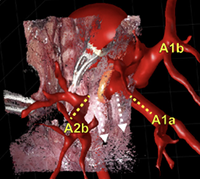
Implementation of delineation error detection systems in time-critical radiotherapy: Do AI-supported optimization and human preferences meet?
Nicolas F. Chaves-de-Plaza, Prerak Mody, Klaus Hildebrandt, Marius Staring, Eleftheria Astreinidou, Mischa de Ridder, Huib de Ridder, Anna Vilanova, René van Egmond
Cognition, Technology & Work (Springer), 2025
[doi]
Improving Uncertainty-Error Correspondence in Deep Bayesian Medical Image Segmentation
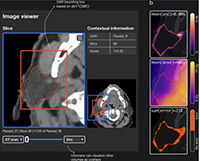
Prerak Mody, Nicolas F. Chaves-de-Plaza, Chinmay Rao, Eleftheria Astrenidou, Mischa de Ridder, Nienke Hoekstra, Klaus Hildebrandt, Marius Staring
Journal of Machine Learning for Biomedical Imaging, 2024
[doi]
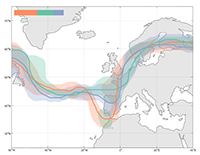
Depth for Multi-Modal Contour Ensembles
Depth for Multi-Modal Contour Ensembles
Nicolas F. Chaves-de-Plaza, Mathijs Molenaar, Prerak Mody, Marius Staring, René van Egmond, Elmar Eisemann, Anna Vilanova, Klaus Hildebrandt
Computer Graphics Forum (EuroVis 2024)
[preprint][doi]
Large-scale dose evaluation of deep learning organ contours in head-and-neck radiotherapy by leveraging existing plans
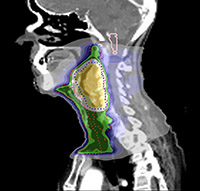
Prerak Mody, Merle Huiskes, Nicolas F. Chaves-de-Plaza, Alice Onderwater, Rense Lamsma, Klaus Hildebrandt, Nienke Hoekstra, Eleftheria Astreinidou, Marius Staring and Frank Dankers
Physics and Imaging in Radiation Oncology, 2024
[preprint][doi]
Accelerating hyperbolic t-SNE
Martin Skrodzki, Hunter van Geffen, Nicolas F. Chaves-de-Plaza, Thomas Höllt, Elmar Eisemann, Klaus Hildebrandt
IEEE Transactions on Visualization and Computer Graphics, 2024
[preprint][doi]
Inclusion Depth for Contour Ensembles
Nicolas F. Chaves-de-Plaza, Prerak Mody, Marius Staring, René van Egmond, Anna Vilanova, Klaus Hildebrandt
IEEE Transactions on Visualization and Computer Graphics, 2024
[preprint][doi]
A Fast Geometric Multigrid Method for Curved Surfaces
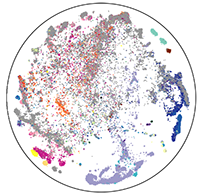
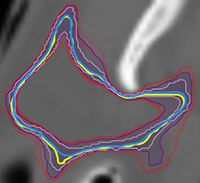
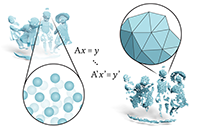
Ruben Wiersma, Ahmad Nasikun, Elmar Eisemann, Klaus Hildebrandt
ACM SIGGRAPH 2023
[preprint][project page][supplementary material][code][doi]
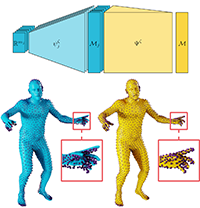
Parametrizing Product Shape Manifolds by Composite Networks
Josua Sassen, Klaus Hildebrandt, Martin Rumpf, Benedikt Wirth
ICLR 2023 spotlight paper (notable top 25%)
[preprint]
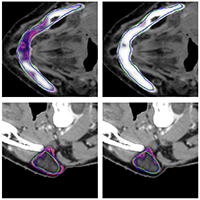
Improving Error Detection in Deep Learning Based Radiotherapy Autocontouring Using Bayesian Uncertainty
Prerak Mody, Nicolas Chaves-de-Plaza, Klaus Hildebrandt, Marius Staring
Uncertainty for Safe Utilization of Machine Learning in Medical Imaging, MICCAI 2022 workshop, Lecture Notes in Computer Science (volume 13563)
[preprint][doi]
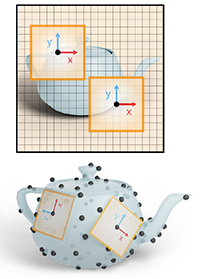
DeltaConv: Anisotropic Operators for Geometric Deep Learning on Point Clouds
Ruben Wiersma, Ahmad Nasikun, Elmar Eisemann, Klaus Hildebrandt
ACM Transactions on Graphics 41(4) (ACM SIGGRAPH 2022)
[preprint][code][project page][doi]
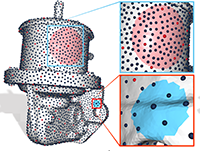
The Hierarchical Subspace Iteration Method for Laplace–Beltrami Eigenproblems
Ahmad Nasikun, Klaus Hildebrandt
ACM Transactions on Graphics 41(2) Article 17, 2022
[preprint][supplementary material][doi]
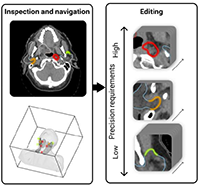
Towards fast human-centered contouring workflows for adaptive external beam radiotherapy
Nicolas F. Chaves-de-Plaza, Prerak Mody, Klaus Hildebrandt, Marius Staring, Eleftheria Astreinidou, Mischa de Ridder, Huib de Ridder, René van Egmond
Human Factors and Ergonomics Society Europe Chapter Annual Conference 2022
[proceedings]
DCGrid: An Adaptive Grid Structure for Memory-Constrained Fluid Simulation on the GPU
Wouter Raateland, Torsten Hädrich, Jorge Alejandro Amador Herrera, Daniel Banuti, Wojciech Palubicki, Sören Pirk, Klaus Hildebrandt, Dominik Michels
Proc. ACM Comput. Graph. Interact. Tech. (I3D 2022)
[preprint][supplementary material][video][code][doi]
Deep vanishing point detection: Geometric priors make dataset variations vanish
Yancong Lin, Ruben Wiersma, Silvia Pintea, Klaus Hildebrandt, Elmar Eisemann, Jan van Gemert
IEEE CVPR 2022
[preprint][doi]
Comparing Bayesian Models for Organ Contouring in Head and Neck Radiotherapy
Prerak Mody, Nicolas Chaves-de-Plaza, Klaus Hildebrandt, Rene van Egmond, Huib de Ridder, Marius Staring
SPIE Medical Imaging 2022: Image Processing
[preprint][doi]
Nonlinear Deformation Synthesis via Sparse Principal Geodesic Analysis
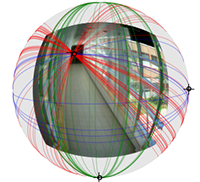
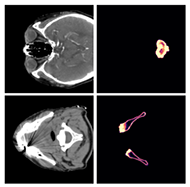
Josua Sassen, Klaus Hildebrandt, Martin Rumpf
Computer Graphics Forum 39(5) (Symposium on Geometry Processing 2020)
[preprint][video][presentation][doi]
CNNs on Surfaces using Rotation-Equivariant Features
Ruben Wiersma, Elmar Eisemann, Klaus Hildebrandt
ACM Transactions on Graphics 39(4) (ACM SIGGRPAH 2020)
[preprint][code][project page][doi]
Locally Supported Tangential Vector, n-Vector, and Tensor Fields
Ahmad Nasikun, Christopher Brandt, Klaus Hildebrandt
Computer Graphics Forum 39(2) (Eurographics 2020)
[preprint][doi]
Geometric Optimization using Nonlinear Rotation-Invariant Coordinates
Josua Sassen, Behrend Heeren, Klaus Hildebrandt, Martin Rumpf
Computer Aided Geometric Design 77, 2020
[preprint][supp. document][video][doi]
The Reduced Immersed Method for Real-Time Fluid-Elastic Solid Interaction and Contact Simulation
Christopher Brandt, Leonardo Scandolo, Elmar Eisemann, Klaus Hildebrandt
ACM Transactions on Graphics 38(6) (ACM SIGGRPAH Asia 2019)
[preprint][video][video (low res.)][code][doi]
A Geometric Optimization Approach for the Detection and Segmentation of Multiple Aneurysms
Kai Lawonn, Monique Meuschke, Ralph Wickenhoefer, Bernhard Preim, Klaus Hildebrandt
Computer Graphics Forum 38(3) (EuroVis 2019), pages 413–425
[preprint][video][supp. document][doi]
Fast Approximation of Laplace–Beltrami Eigenproblems
Ahmad Nasikun, Christopher Brandt, Klaus Hildebrandt
Computer Graphics Forum 37(5) (Symposium on Geometry Processing 2018), pages 121–134
[preprint][supp. document][video 1][video 2][code][doi]
Hyper-Reduced Projective Dynamics
Christopher Brandt, Elmar Eisemann, Klaus Hildebrandt
ACM Transactions on Graphics 37(4) Article 80 (ACM SIGGRAPH 2018)
[preprint][video][video (low res.)][supp. material][demo][code][doi]
Modeling n-Symmetry Vector Fields using Higher-Order Energies
Christopher Brandt, Leonardo Scandolo, Elmar Eisemann, Klaus Hildebrandt
ACM Transactions on Graphics 37(2) Article 18, 2018 - Presented at ACM SIGGRAPH 2018
[preprint][video][doi]
A Formalization of Relative Local Tempo Variations in Collections of Performances
Jeroen Peperkamp, Klaus Hildebrandt, Cynthia C. S. Liem
Proceedings of International Society for Music Information Retrieval Conference (ISMIR) 2017 - Selected for oral presentation
[paper]
Compressed Vibration Modes of Elastic Bodies
Christopher Brandt, Klaus Hildebrandt
Computer Aided Geometric Design 52–53 (Geometric Modeling and Processing 2017), pages 297–312
[preprint][video][doi]
Spectral Processing of Tangential Vector Fields
Christopher Brandt, Leonardo Scandolo, Elmar Eisemann, Klaus Hildebrandt
Computer Graphics Forum 36(6), pages 338–353, 2017 - Presented at Eurographics 2017
[preprint][video][supp. material][doi]
Visualization and Extraction of Carvings for Heritage Conservation
Kai Lawonn, Erik Trostmann, Bernhard Preim, Klaus Hildebrandt
IEEE Transactions on Visualization and Computer Graphics 23(1), pages 801–810, 2017 (IEEE Visualization 2016)
[preprint][doi]
Optimized Subspaces for Deformation-Based Modeling and Shape Interpolation
Philipp von Radziewsky, Elmar Eisemann, Hans-Peter Seidel, Klaus Hildebrandt
Computers & Graphics 58 (Shape Modeling International 2016), pages 128–138
Best Paper Award at Shape Modeling International 2016
[preprint][video][doi]
Geometric Flows of Curves in Shape Space for Processing Motion of Deformable Objects
Christopher Brandt, Christoph von Tycowicz, Klaus Hildebrandt
Computer Graphics Forum 35(2) (Eurographics 2016), pages 295–305
Best Paper Honorable Mention Award at Eurographics 2016
[preprint][video][doi]
Directional Field Synthesis, Design, and Processing
Amir Vaxman, Marcel Campen, Olga Diamanti, Daniele Panozzo, David Bommes, Klaus Hildebrandt, Mirela Ben-Chen
Computer Graphics Forum 35(2) (STAR -- Eurographics 2016), pages 545–572
[preprint][doi]
Foldio: Digital Fabrication of Interactive and Shape-Changing Objects With Foldable Printed Electronics
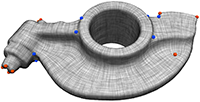
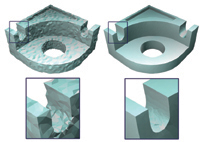
Simon Olberding, Sergio Soto Ortega, Klaus Hildebrandt, Jürgen Steimle
ACM Symposium on User Interface Software and Technology (UIST) 2015
Best Paper Award at UIST 2015
Selected for the UIST reprise session at SIGGRAPH 2016
[preprint][video][doi]
Animating Articulated Characters using Wiggly Splines
Christian Schulz, Christoph von Tycowicz, Hans-Peter Seidel, Klaus Hildebrandt
ACM SIGGRAPH/Eurographics Symposium on Computer Animation 2015, pages 101–109
[preprint][video][doi]
Real-Time Nonlinear Shape Interpolation
Christoph von Tycowicz, Christian Schulz, Hans-Peter Seidel, Klaus Hildebrandt
ACM Transactions on Graphics 34(3) Article No. 34 - Presented at ACM SIGGRAPH 2015
[preprint][video][doi]
Optimal Spline Approximation via l0-Minimization
Christopher Brandt, Hans-Peter Seidel, Klaus Hildebrandt
Computer Graphics Forum 34(2) (Eurographics 2015), pages 617–626
[preprint][video][doi]
3D Model Retargeting Using Offset Statistics
Xiaokun Wu, Chuan Li, Michael Wand, Klaus Hildebrandt, Silke Jansen, Hans-Peter Seidel
Proceedings of the 2nd International Conference on 3D Vision 2014, IEEE, pages 353–360
[preprint][video][doi]
Real-Time Symmetry-Preserving Deformation
Xiaokun Wu, Michael Wand, Klaus Hildebrandt, Pushmeet Kohli, Hans-Peter Seidel
Computer Graphics Forum 33(7) (Pacific Graphics 2014), pages 229–238.
[preprint][video][doi]
Animating Deformable Objects using Sparse Spacetime Constraints
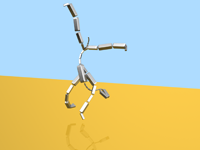
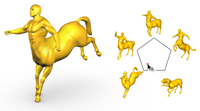
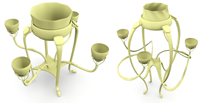
Christian Schulz, Christoph von Tycowicz, Hans-Peter Seidel, Klaus Hildebrandt
ACM Transactions on Graphics 33(4) (SIGGRAPH 2014) Article No. 109
[preprint][video][supplementary material][doi]
An Efficient Construction of Reduced Deformable Objects
Christoph von Tycowicz, Christian Schulz, Hans-Peter Seidel, Klaus Hildebrandt
ACM Transactions on Graphics 32(6) (SIGGRAPH Asia 2013) Article No. 213
[preprint][video][doi]
Interactive spacetime control of deformable objects
Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
ACM Transactions on Graphics 31(4) (SIGGRAPH 2012) Article No. 71
[preprint][video][doi]
Interactive Surface Modeling using Modal Analysis
Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
ACM Transactions on Graphics 30(5), pages 119:1–119:11, 2011 - Presented at ACM SIGGRAPH 2012
[preprint][video][doi]
Modal Shape Analysis beyond Laplacian
Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
Computer Aided Geometric Design 29(5), pages 204–218, 2012
[preprint][video][doi]
Generalized Shape Operators on Polyhedral Surfaces
Klaus Hildebrandt, Konrad Polthier
Computer Aided Geometric Design 28(5), pages 321–343, 2011
[preprint][doi]
On approximation of the Laplace–Beltrami operator and the Willmore energy of surfaces
Klaus Hildebrandt, Konrad Polthier
Computer Graphics Forum 30(5), 2011, pages 1513–1520
1st-Prize Best Paper at the ACM Siggraph/Eurographics Symposium on Geometry Processing 2011
[preprint][doi]
Koiter's Thin Shells on Catmull–Clark Limit Surfaces
Anna Wawrzinek, Klaus Hildebrandt, Konrad Polthier
Vision, Modeling, and Visualization 2011
[preprint][doi]
Eigenmodes of surface energies for shape analysis
Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
Advances in Geometric Modeling and Processing, Lecture Notes in Computer Science 6130, Springer, pages 296–314.
Proceedings of Geometric Modeling and Processing 2010
[preprint][doi]
Constraint-based fairing of surface meshes
Klaus Hildebrandt, Konrad Polthier
Symposium on Geometry Processing 2007
[preprint][doi]
On the Convergence of Metric and Geometric Properties of Polyhedral Surfaces
Klaus Hildebrandt, Konrad Polthier, Max Wardetzky
Geometriae Dedicata, 123, 89–112, 2006
[preprint][doi]
Smooth Feature Lines on Surface Meshes
Klaus Hildebrandt, Konrad Polthier, Max Wardetzky
Symposium on Geometry Processing 2005
[preprint][doi]
Anisotropic Filtering of Non-Linear Surface Features
Klaus Hildebrandt, Konrad Polthier
Computer Graphics Forum, 23(3), 391–400,2004
1st-Prize Best Student Paper Award at Eurographics 2004
[preprint][videos][doi]