Source selection for the direct lighting computation in global illumination [1]

 

Arjan J.F. Kok and Frederik W. Jansen

 

Computation of the global illumination in a scene can be improved by separating the direct component of the lighting, that is received by a patch directly from light sources, from the indirect component that is received by intermediate interreflection from other patches. The indirect component is calculated during the preprocessing and is stored as the radiosity shading at the patch. The direct component is re-calculated during the rendering phase by tracing shadow rays like in conventional ray tracing. The number of shadow rays can be reduced by exploiting shadow coherence, and by making a selection for the number of light sources that are taken into account for the direct lighting computation. Different criteria to select these sources are given.

 

Key words: radiosity, global illumination, source sampling

1.   Introduction

Highly realistic images can be generated by two-pass radiosity algorithms (Wallace et al 1987; Sillion and Puech 1989) that calculate, in a preprocessing step the diffuse component of the light reflection on a patch. During the rendering phase, the specular component of the reflection is added by ray tracing. A problem with these algorithms is to represent accurately the preprocessed radiosity shading because it often shows much variation over the patch. This is mainly due to the light that is received directly from strong (point) light sources, and that is responsible for sharp shadows. To represent these intensity variations, the patches can be further subdivided into elements. However, it is nearly impossible to find a good subdivision scheme that represents the shadows accurately. Methods such as adaptive patch refinement (Cohen et al 1986) and shadow meshes (Campbell and Fussell 1990) require large data structures and fail to provide the dynamic adaptation that is needed, for instance, when one zooms in on a single patch in a very large scene. The use of adaptive radiosity textures (rexes) in combination with a viewpoint dependent preprocessing that restricts the preprocessing to those patches that are prominent in a given view (Heckbert 1990), reduces the problem, but does not solve it.

 

A solution to the problem is to make a distinction between light that is received directly and light that is received indirectly from light sources (Ward et al 1988; Shirley 1990). Direct light is light that a patch receives from a light source (a light emitting patch or a strong radiant patch) without being reflected by other patches. Indirect light is the light that is received after one or more (diffuse or specular) reflections. In Shirley's approach, during the preprocessing step (illumination ray tracing and radiosity) only the diffuse reflection of the indirectly received light is calculated for each patch and stored as illumination maps and the radiosity shading on the patch. To calculate the radiosity component, first the complete global illumination problem is solved, and then the direct lighting component is subtracted from the total radiosity shading. The resulting radiosity shading will show only minor intensity variations over a patch. Therefore, patch refinement can be relatively coarse.

 

During the rendering phase, the indirect lighting reflection component for a point on a patch is calculated by interpolating the radiosity shading values that are pre-calculated for the vertices of the patch. The direct component is added by calculating the contribution of the light sources by casting shadow rays to the light sources. For small sources, one shadow ray suffices, whereas for large light sources, more shadow rays are needed to obtain soft shadows. The result of this two pass global illumination method is a realistic image, that combines the best qualities of ray tracing and radiosity.

A drawback of the algorithm is that the number of shadow rays can be very large, especially when there are many area light sources. It is clear that the calculation of the direct component in these cases will be expensive and will require extra ray tracing compared to the conventional two pass methods. Therefore methods for reducing the number of shadow rays are needed. Shirley (1990) uses a form of path tracing (Kajiya 1986), in which only one shadow ray is cast to a light source for each ray-surface intersection. To which light source the shadow ray is cast is governed by the probabilities assigned to the sources. This stochastic method has the drawback, that a large number of samples for each pixel is necessary to get reliable results. Another way to reduce the number of shadow rays is to use shadow coherence. We used an adaptive image refinement method in combination with a shadow image buffer (Woodward 1990; Kok et al 1991).

 

A third approach would be to limit the number of light sources to be considered for direct lighting and to add the contribution of the less prominent light sources to the indirect component. Proper selection of the most important light sources during the rendering could reduce the number of shadow rays without loss of shading accuracy. This approach will be explored in this paper.

In section 2 we will discuss criteria to select the light sources. Section 3 gives a description of the implementation of the two pass global illumination method. The results of our experiments are presented in section 4. Conclusions and future directions are given in section 5.

2. Source selection

In radiosity algorithms, all patches in a scene are considered as possible light sources. A radiosity preprocessing is applied to calculate for each patch the diffuse component of the reflection. However, by treating the very important contribution of the strongest light sources in the same way as the light from the other patches, a loss of shadow accuracy occurs, resulting in very smoothed pictures, which in fact can be very unrealistic. The basic idea of Shirley's algorithm (1990) is, therefore, to handle the most important light sources as in conventional ray tracing, and to handle the other light sources (and other radiant patches) as with the conventional two pass radiosity methods. The light received directly from strong light sources is sampled by shooting shadow rays, while the light received from the other patches is calculated during the preprocessing step, and is stored as the radiosity shading on the patches.

 

The question is: which light sources should be considered for the direct lighting computation? If all patches are considered as light sources, then this would result in far too many shadow rays. If only a limited number of light sources is considered then the shadow accuracy will be low. A related problem is: how many shadow rays will be needed for area light sources? A large number will be expensive, while fewer rays will result in shadows that are too sharp compared to the soft shadows that may be expected from area light sources.

 

An obvious choice for the light source selection is to take the n most emitting or most radiant patches, i.e. the first n patches that are selected in the progressive refinement (shooting) radiosity method. However, this global selection neglects the fact that a light source can have a strong effect on some patches, but may have a negligible influence on other patches. Therefore it is better to make a local selection, i.e. select for each patch the n most important light sources. We now give some criteria to select a patch j to be a light source for patch i.

If the energy received by patch i, coming from patch j, is larger then a certain threshold value, then patch j is considered as a possible light source. We call this the radiance criterion. Therefore, the n most important contributions to the shading of a patch will have to be stored separately at the patch.

 

The second aspect is the diffuse reflectivity of the patch. The reflected intensity, and so the shadow contrast is not only dependent on the received energy, but is also dependent on the amount of light that is diffusely reflected by the patch. It is, for example, not necessary to cast shadow rays from a patch for which the diffuse reflectivity is almost zero (for example a perfect specular reflective patch), although it receives a lot of energy from patch j. So if the reflected intensity of patch i caused by the energy received from patch j is larger then a certain threshold, then patch j is considered to be a light source. We call this the reflectivity criterion.

 

Although the intensity of the received light is important, for finding possible shadows on a patch the distribution of the light over that patch is also important. If the light coming from patch j gives large intensity variations over patch i, then patch j should be considered as a light source for patch i. At the other hand if it can be detected a priori that the light from a strong light source shines on the whole patch i or does not reach patch i at all, then the contribution of patch j, if any, can be added to the pre-calculated radiosity shading. We will call this the gradient criterion. To detect gradients we have to compute the contributions for patch j to patch i at different points on patch i . If these contributions show large differences, then some kind of shadow or shading boundary will appear on this patch, and then the light source should be sampled with shadow rays during rendering. Of course, as with all coherence methods, care should be taken not to miss small shadows.

 

Another aspect of the light source selection is related to the number of shadow rays that will have to be cast. If a possible light source (patch j) is small (e.g. is a point light source) or is seen with a small solid angle from patch i, then only one shadow ray will be needed. Shadow rays are then effective, and patch j is likely to be chosen as a light source. If, however, the possible light source is an area light source, and the solid angle is large, then a soft shadow is expected which can be represented much better with the radiosity shading. So, based on the solid angle it is determined whether shadow rays will be cast, and if so, how many shadow rays will be cast. We call this criterion the solid angle criterion.

 

Finally, it may be observed that patches farther away from the viewer are not so critical for the perceived image quality. A more approximated shadow computation can be accepted and the number of shadow rays can be reduced or the shadow ray casting can be limited to only the most important light sources (the contribution of the other light sources are added to the general radiosity). We will call this the distance criterion.

 

If a local selection is used for the selection of the sources and/or the number of shadow rays, care should be taken that patch boundaries do not become visible due to differences between neighbouring patches in the selection of light sources. It is therefore advisable to apply a selection only to a cluster of patches (object) instead of to a single patch.

Given the described criteria, an optimum combination of these criteria must be derived taking into account the radiance of all patches, the viewpoint, etc.

3. Implementation

To calculate the indirect reflection component in the preprocessing, both the full-matrix (gathering) method (Cohen and Greenberg 1985) and the progressive refinement (shooting) method (Cohen et al 1988) can be used. If the full-matrix method is used, the choice of the most important light sources can be made after calculation of the formfactors. This can be done as follows:

1.      Calculate all formfactors.

2.      Solve the complete system of equations.

3.      Choose the most important sources.

4.      Set formfactors representing indirect light transport to zero (the formfactors F, where patch i and patch j are not chosen as light sources).

5.      Solve the system of equations again. This will result in the direct reflection components.

6.      Subtract the radiosity values calculated in step 5 from the values calculated in step 2. The resulting radiosity values are the indirect reflection components.

 

A disadvantage of this approach is that difficulties arise when specular reflections (use of extended formfactors) must be included in the calculation. The progressive refinement (shooting) method is therefore more suited. On basis of the progressive refinement radiosity method we propose the following source selection algorithm.

 

During the preprocessing the radiosities for all patches in the scene are calculated. The radiosities are stored at the patch vertices (several points on the patch). To be able to make a selection of light sources for the direct lighting computation, for each patch vertex, in addition to a general radiosity value, a list is maintained that contains the contributions of the n most important light sources (based on the radiance criterion). Contributions that fail to enter this list (contributions from less influential sources) are added to the general radiosity value. The number n must not be chosen too small, to be able to make a good selection before rendering.

After the shooting is done, a further selection of light sources is made based on the reflectivity criterion, the gradient criterion and the solid angle criterion. The gradient criterion is applied by comparing the contributions of the possible light sources (stored in the list) at two neighbouring vertices. If there is a large difference between the contributions, then the possible light source will be chosen. With the solid angle criterion also the number of shadow rays that will have to be cast from the patch to the light source can be determined.

 

Prior to the rendering an additional viewpoint-dependent selection can be made based on the distance criterion (some patches that first were selected as sources can be omitted, or the number of needed shadow rays can be changed). The above selection reduces the number of lightsources to m (m <= n, m is not constant for all patches if a local selection is used). The other n - m contributions (of less influential sources) are added to the general radiosity.

 

For the rendering, an adaptive stochastic ray tracing algorithm (Dippé and Wold 1985; Cook 1986; Mitchell 1987; Painter and Sloan 1989) is used. Viewing rays are traced from the eye through the viewing plane into the scene. If a viewing ray hits a patch, the indirect reflection component is calculated by interpolation from the general vertex radiosity values. The direct component, due to the m selected light source patches, is calculated by casting shadow rays.

 

First the scene is sampled at a low resolution. After the first sampling, the screen sampling is adaptively refined. Shadow rays are cast adaptively too, using a shadow image buffer (Woodward 1990; Kok et al 1991) that serves to indicate whether neighbouring samples (viewing rays) have the same shadow properties (sample in shadow or in light; the shadow image buffer stores at each sample one bit for each light source). Shadow rays are sent to jittered points on area light sources to avoid aliasing. The following criteria are successively applied to sample the screen adaptively:

1)      Object criterion. If neighbouring samples do not all hit the same object, extra samples are taken to discover the exact object boundaries.

2)      Shadow criterion. If neighbouring samples do not show the same shadow property (all light or all shadow), then a shadow boundary exists, and extra samples are taken in this region to find the exact shadow boundaries.

3)      Difference (gradient) criterion. If the intensity of neighbouring samples (pixels) differs more than a certain threshold, then extra samples are taken. By using shadow coherence, no extra shadow rays are needed in this case.

When all refinement criteria are satisfied, or a maximum sampling rate is reached, the pixel values are calculated using filtering techniques.

4. Experiments

We tested different light source selections to see the influence of the selection on the quality of the image and the number of shadow rays needed. All tests were done on the scene of figure 1. The scene contains two spot light sources A and B (on the corners on the right, pointing to the table) and two area light sources C (on the ceiling) and D (on the left wall).

 

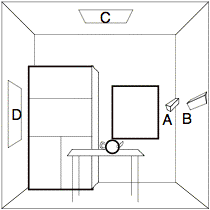
Figure 1. Sketch of test scene.

 

Several images were created with different selections of sources, using the same preprocessing. The results are given in table 1 (image size 256x256).

The radiosity solution (a) misses shadow details. The shadow of the handle of the teapot and the shadows of the table legs are missing. A very fine subdivision of the patches could solve this, but will cost a lot of memory and processing time. For the two spot light sources, one shadow ray is sufficient (b). For the area light sources, more shadow rays per source are needed (d-h). For light source C, 16 shadow rays are needed to get a good shadow on the table, but for other patches in the environment, smaller numbers (or even 0) will suffice. For light source D, 64 rays are needed to get soft shadows on the floor, but for the table only 16 (or even 4) shadow rays are sufficient. So, local selection criteria to determine the number of shadow rays for each light source can strongly reduce the number of shadow rays.

The number of shadow rays is always much smaller than the number of viewing rays times the number of the shadow rays per sample, because no shadow rays are cast for patches that are backfacing with respect to a light source, and because the program exploits shadow coherence (the reduction approaches a total of 90%).

 

Table 1. Number of viewing and shadow rays for different source selections.

 

We are currently implementing algorithms to automatically apply the described local criteria to obtain high-quality pictures with a minimum of shadow rays.

5. Conclusions and directions for future research

The experiments show that the described method is able to represent sharp shadow, because of the separation of the direct and indirect shading over the two passes. By proper selection of light sources for shadow testing the images will be generated efficiently.

Different criteria for selecting the most influential light sources were given. All experiments so far were done with a global selection of light sources. Use of local selections will further reduce the number of shadow rays. A disadvantage of the given method is the extra memory required to store the influences of the most important light sources separately at each patch vertex.

Compared to statistical methods to reduce the number of shadow rays (Kajiya 1986; Shirley 1990), for which a lot of viewing rays per pixel are necessary to get reliable results, the presented method will also be useful if only a few viewing rays per pixel are used.

Acknowledgements

This research is part of the radiosity engine project, a cooperation with the Network Theory section of the Faculty of Electrical Engineering at Delft University of Technology. We thank Ed Deprettere and Li-Sheng Shen for the discussions on radiosity methods.

References

Campbell, A.T., Fussell, D.S. (1990) "Adaptive Mesh Generation for Global Diffuse Illumination", Computer Graphics 24(4), pp 155-164, Siggraph '90.

Cohen, M. F., Greenberg, D. P. (1985) "The hemi-cube: A Radiosity Solution for Complex Environments", Computer Graphics 19(3), pp 31-40, Siggraph '85.

Cohen, M.F., Greenberg, D.P., Immel, D.S., Brock, P.J. (1986) "An Efficient Radiosity Approach for Realistic Image Synthesis", IEEE Computer Graphics and Applications 6(3), pp 26-35.

Cohen, M.F., Cheng, S.E., Wallace, J.R., Greenberg, D.P. (1988) "A Progressive Refinement Approach to Fast Radiosity Image Generation", Computer Graphics 22(4), pp 75-84, Siggraph '88.

Cook, R.L. (1986) "Stochastic Sampling in Computer Graphics", ACM Transactions on Graphics 5(1), pp 51-72.

Dippé, M., Wold, E. H. (1985) "Antialiasing through Stochastic Sampling", Computer Graphics 19(3), pp 69-78, Siggraph '85.

Heckbert, P.S. (1990) "Adaptive Radiosity Textures for Bidirectional Ray Tracing", Computer Graphics 24(4), pp 145-154, Siggraph '90.

Kajiya, J.T. (1986) "The Rendering Equation", Computer Graphics 20(4), pp 143-150, Siggraph '86.

Kok, A.J.F., Jansen, F.W., Woodward, C. (1991) "Efficient Complete Radiosity Ray Tracing using a Shadow Coherence Method", submitted for publication.

Mitchell, D. P. (1987) "Generating Antialiased Images at Low Sampling Densities", Computer Graphics 21(4), pp 65-72, Siggraph '87.

Painter, J., Sloan, K. (1989) "Antialiased Ray Tracing by Adaptive Progressive Refinement", Computer Graphics 23(3), pp 281-288, Siggraph '89.

Shirley, P. (1990) "A Ray Tracing Method for Illumination Calculation in Diffuse Specular Scenes", Proceedings Computer Graphics Interface '90, pp 205-212.

Sillion, F., Puech, C. (1989) "A General Two Pass Method Integrating Specular and Diffuse Reflec­tion", Computer Graphics 23(3), pp 335-344, Siggraph '89.

Wallace, J.R., Cohen, M.F., Greenberg, D.P. (1987) "A Two-Pass Solution to the Rendering Equation: A Synthesis of Ray Tracing and Radiosity Methods", Computer Graphics 21(4), pp 311-320, Siggraph '87.

Ward, G.J., Rubinstein, F.M., Clear, R.D. (1988) "A Ray Tracing Solution for Diffuse Interreflection", Computer Graphics 22(4), pp 85-92, Siggraph '88.

Woodward, C. (1990) "Methods for Computer-Aided Design of Free-form Objects, PhD thesis, Helsinki University of Technology, Acta Polytechnica Scandinavica, Mathematics and Computer Science Series No. 56, Finnish Academy, Helsinki.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Picture 1a-d

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Picture 1e-h