DeltaConv: Anisotropic Operators for Geometric Deep Learning on Point Clouds

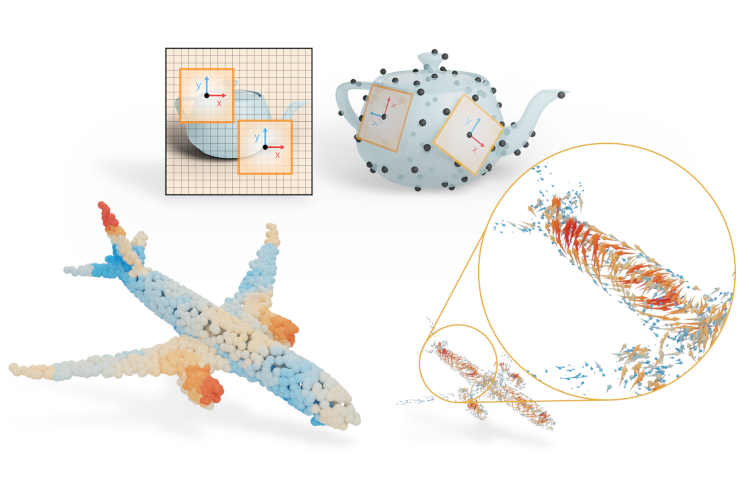
Learning from 3D point-cloud data has rapidly gained momentum, motivated by the success of deep learning on images and the increased availability of 3D data. In this paper, we aim to construct anisotropic convolution layers that work directly on the surface derived from a point cloud. This is challenging because of the lack of a global coordinate system for tangential directions on surfaces. We introduce DeltaConv, a convolution layer that combines geometric operators from vector calculus to enable the construction of anisotropic filters on point clouds. Because these operators are defined on scalar- and vector-fields, we separate the network into a scalar- and a vector-stream, which are connected by the operators. The vector stream enables the network to explicitly represent, evaluate, and process directional information. Our convolutions are robust and simple to implement and match or improve on state-of-the-art approaches on several benchmarks, while also speeding up training and inference.

@Article { WNEH22,
  author       = "Wiersma, Ruben and Nasikun, Ahmad and Eisemann, Elmar and Hildebrandt, Klaus",
  title        = "DeltaConv: Anisotropic Operators for Geometric Deep Learning on Point Clouds",
  journal      = "ACM Trans. Graph. (Proc. of SIGGRAPH)",
  number       = "4",
  volume       = "41",
  pages        = "105:1--105:13",
  month        = "jul",
  year         = "2022",
  doi          = "10.1145/3528223.3530166",
  note         = "Project page: https://rubenwiersma.nl/deltaconv",
  url          = "http://graphics.tudelft.nl/Publications-new/2022/WNEH22"
}