The Hierarchical Subspace Iteration Method for Laplace–Beltrami Eigenproblems

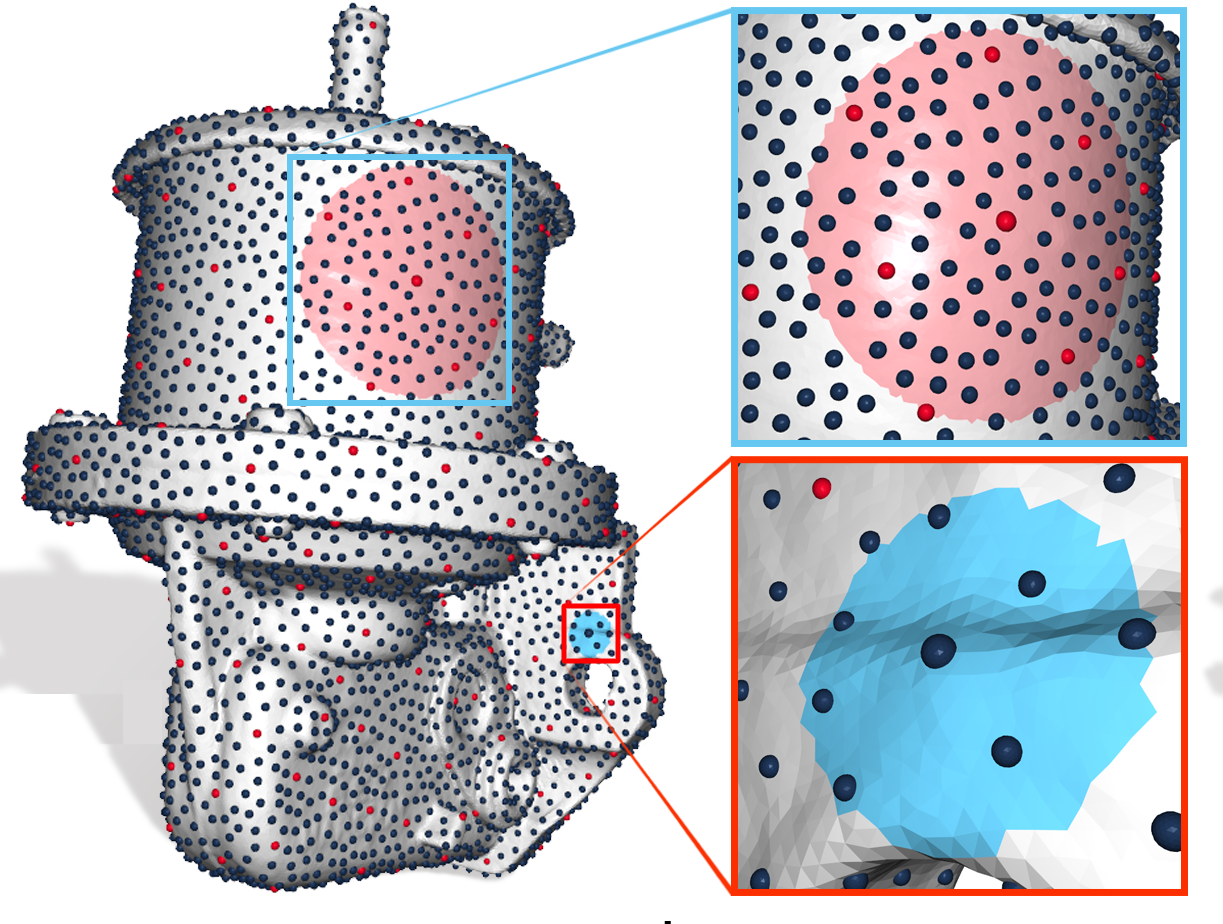
Sparse eigenproblems are important for various applications in computer graphics. The spectrum and eigenfunctions of the Laplace--Beltrami operator, for example, are fundamental for methods in shape analysis and mesh processing. The Subspace Iteration Method is a robust solver for these problems. In practice, however, Lanczos schemes are often faster. In this paper, we introduce the Hierarchical Subspace Iteration Method (HSIM), a novel solver for sparse eigenproblems that operates on a hierarchy of nested vector spaces. The hierarchy is constructed such that on the coarsest space all eigenpairs can be computed with a dense eigensolver. HSIM uses these eigenpairs as initialization and iterates from coarse to fine over the hierarchy. On each level, subspace iterations, initialized with the solution from the previous level, are used to approximate the eigenpairs. This approach substantially reduces the number of iterations needed on the finest grid compared to the non-hierarchical Subspace Iteration Method. Our experiments show that HSIM can solve Laplace--Beltrami eigenproblems on meshes faster than state-of-the-art methods based on Lanczos iterations, preconditioned conjugate gradients and subspace iterations.

@Article { NH22,
  author       = "Nasikun, Ahmad and Hildebrandt, Klaus",
  title        = "The Hierarchical Subspace Iteration Method for Laplace–Beltrami Eigenproblems",
  journal      = "ACM Transactions on Graphics",
  number       = "2",
  volume       = "41",
  pages        = "17.1--17.14",
  year         = "2022",
  doi          = "https://doi.org/10.1145/3495208",
  url          = "http://graphics.tudelft.nl/Publications-new/2022/NH22"
}