CNNs on Surfaces using Rotation-Equivariant Features

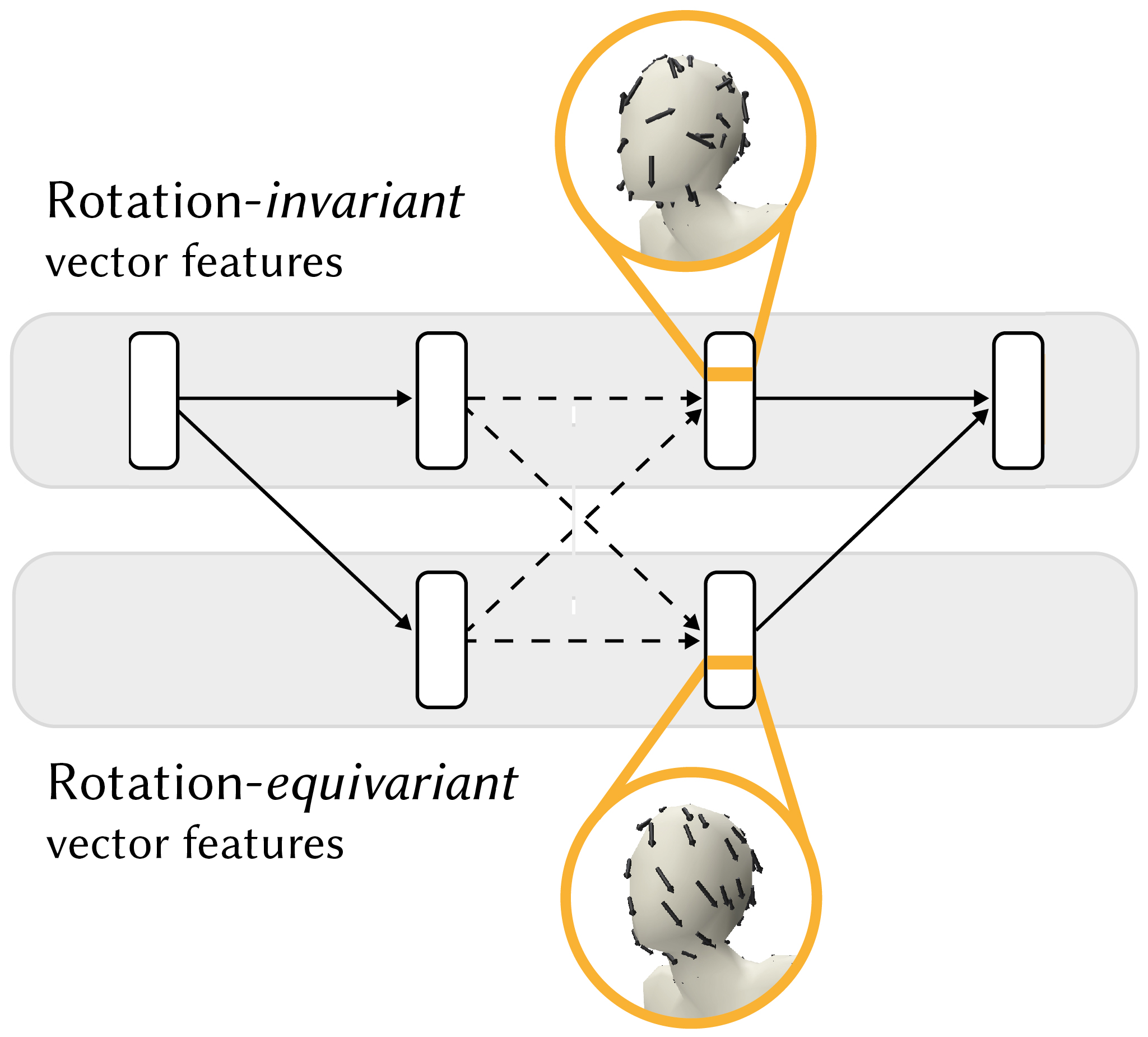
This paper is concerned with a fundamental problem in geometric deep learning that arises in the construction of convolutional neural networks on surfaces. Due to curvature, the transport of filter kernels on surfaces results in a rotational ambiguity, which prevents a uniform alignment of these kernels on the surface. We propose a network architecture for surfaces that consists of vector-valued, rotation-equivariant features. The equivariance property makes it possible to locally align features, which were computed in arbitrary coordinate systems, when aggregating features in a convolution layer. The resulting network is agnostic to the choices of coordinate systems for the tangent spaces on the surface. We implement our approach for triangle meshes. Based on circular harmonic functions, we introduce convolution filters for meshes that are rotation-equivariant at the discrete level. We evaluate the resulting networks on shape correspondence and shape classifications tasks and compare their performance to other approaches.

@Article { WEH20,
  author       = "Wiersma, Ruben and Eisemann, Elmar and Hildebrandt, Klaus",
  title        = "CNNs on Surfaces using Rotation-Equivariant Features",
  journal      = "ACM Transactions on Graphics (Proc. of SIGGRAPH)",
  number       = "4",
  volume       = "39",
  year         = "2020",
  doi          = "10.1145/3386569.3392437",
  note         = "Code at github.com/rubenwiersma/hsn",
  url          = "http://graphics.tudelft.nl/Publications-new/2020/WEH20"
}